Countable and uncountable sets, part 2

When we last looked at countable and uncountable sets, we defined countable sets as those for which we can make a one-to-one correspondence between the set and the natural numbers, and that, therefore, have the same cardinal number as the natural numbers: . And we found that the even numbers, the whole numbers, and the integers are all countable.

Let’s look at one more, the set of rational numbers.

The rational numbers are the set of all fractions... that is, the set of all numbers that can be written as a/b, where a is an integer and b is a natural number. We seem to be going up by an order of magnitude here; surely there’s no one-to-one mapping from the natural numbers to the rationals, is there?

There is. To make it easier, we’ll observe that the existence of a one-to-one correspondence is transitive, so we can use the integers instead of the natural numbers (since we already have a one-to-one correspondence there). We’ll again map 0 to 0, and we’ll map each negative integer to a negative rational in the same manner as with the positive numbers. How we’ll map the positive numbers, then, needs some explanation.

Write the positive integers, the tops of the fractions, as the headings of the columns of an infinite table. Write the natural numbers, the bottoms of the fractions, as the rows of the table. In each cell of the table, write the resulting fraction. We get this:

	1	2	3	4	5	6	...
1	1/1	2/1	3/1	4/1	5/1	6/1
2	1/2	2/2	3/2	4/2	5/2	6/2
3	1/3	2/3	3/3	4/3	5/3	6/3
4	1/4	2/4	3/4	4/4	5/4	6/4
...

If we traverse this table by upper-right to lower-left diagonals, skipping the fractions that are not reduced (and are, therefore, duplicates — 2/2 and 3/3 are the same as 1/1; 2/4 is the same as 1/2), we get this mapping:

1 maps to 1/1, 2 maps to 2/1, 3 maps to 1/2, 4 maps to 3/1,
5 maps to 1/3, 6 maps to 4/1, 7 maps to 3/2, 8 maps to 2/3,
9 maps to 1/4, 10 maps to 5/1, 11 maps to 1/5, ...

That mapping is easily proved to fit the bill: the rational numbers are, indeed, countable — their cardinal number is also .

Now, that one is really counter-intuitive. The rational numbers are densely ordered: between any two rational numbers, there’s another rational number. In fact, cascading that aspect infinitely, it means that between any two rational numbers, there’s a countably infinite number of rationals. The natural numbers, on the other hand, are not dense — there’s no natural number between 1 and 2, for instance. And, yet, they have the same cardinality

Think about what that means. The following sets all have the same cardinal number, — they are all, in a sense, the “same size”:

• The set of natural numbers.
• The set of integers.
• The set of rational numbers.
• The set of rational numbers between 1 and 2.
• The set of rational numbers between ¼ and ½
• For any two rational numbers, a < b, however small the difference between them, the set of rational numbers between a and b.

One more thing, then, which we’ll state without proving (it should be intuitively clear): any subset of a countable set is countable.

Let’s move on to the real numbers: the union of the rational numbers — those that can be represented as fractions of integers — and the irrational numbers, numbers such as √2, √3, and π, which can not be represented as fractions. Non-rigorously, it’s the set of all numbers that can be represented with (possibly infinite) decimal representations. 3 (or 3.0, or ...00003.0000..., a natural number). 3.1 (31/10, a rational number). 3.142857[142857]... (22/7, a rational number). 3.14159265... (π, an irrational number). And so on.

A rigorous definition of the set of real numbers involves definitions of properties and operations, and concepts of group theory that are beyond our scope here, so we’ll have to stay with the intuitive description.

What’s the cardinality of the set of real numbers? Is its cardinal number also ? Is the set of real numbers countable?

As it turns out, it’s not. The mathematician Georg Cantor is credited with proving that in 1874, but his more famous demonstration of it, the Cantor diagonal, was published more than 15 years later.

Here’s an understandable (I hope!) explanation of Cantor’s argument, using the “infinite decimal representation” intuition: Suppose we do have a one-to-one correspondence between the natural numbers and the real numbers. That means that for any natural number n, there is a corresponding real number r. Let’s call that mapping f, so f(n) = r. Since r can be written in a decimal representation as an infinite sequence of digits, we can look at the nth digit. So let’s construct a real number q this way: make the first digit different from the first digit in f(1); make the second digit different from the second digit in f(2); ... in general, make the nth digit different from the nth digit in f(n).

It should be clear that q must be different from any of the numbers that appear in {f(n), for all natural numbers n}, because it always differs from the nth number in the nth decimal place. It’s therefore not possible for any chosen f(n) to be a one-to-one mapping, because we can always find such an exception.

Another fact about cardinality is that for any set S, its power set (the set of its subsets), P(S), has a cardinal number that’s strictly greater than the cardinal number of S. This is intuitively true for finite sets, of course (try it, and remember that the empty set is a subset of any set), but Cantor’s diagonal argument proved it for all sets. It turns out, then, that the power set of the natural numbers has the same cardinality as does the set of real numbers. (It also means that there are at least a countably infinite number of cardinal numbers above , because we can keep taking the power set of the power set of the power set... to get larger and larger alephs.

What, then, is the cardinal number of the real numbers? Is there a concept of a “next” aleph, or is the set of alephs dense? If there is a next aleph, is that the cardinal number of the reals?

There is, in fact, a next aleph, and we have , , and so on, so that there’s an 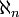for any whole number n. Even beyond that, there are more, but we’re getting into other areas now, and it’ll get hopelessly confusing.

So, back to the other question at hand: is the cardinal number of the set of real numbers equal to ? Well, the fact is that we don’t know — we can’t prove it either way. We can say that the cardinality of the reals is 2 to the power of , but we can’t say what that is, in our sequence of alephs. We can, in fact, consistently assume the cardinality of the real numbers to be any 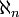, for any natural number n. I find that to be very cool.

Now, since we can assume any, if we choose to assume that the cardinality of the set of real numbers is we get Cantor’s continuum hypothesis (and, again, remembering that in all of this we’re also assuming the axiom of choice).

I think that’s all I want to say about countability and cardinality. If you think, as I do, that this is fascinating, read more about Georg Cantor and his work, and the work that came after.