Recently, I was discussing the relative virtues of four-door and two-door cars with a friend. I prefer four-door cars, because they make it much easier for back-seat passengers to get in and out (they make it easier to access the back seat, in general). My friend prefers two-door cars, because he seldom has back-seat passengers, and the larger doors of two-door cars make it easier for the front-seat occupants to get in and out.
“But,” I say, “on a two-door car, the doors are larger and heavier. Also, if you’re in a limited space, the doors can’t open as far, and the smaller opening actually makes it harder for the people in the front seat.”
I also recently read Kate Nowak’s post “Introducing Right Triangle Trig”, from her blog f(t) [Function of Time].[1]
Putting the two together, I thought it would be fun[2] to turn the car-door discussion into a trig problem.
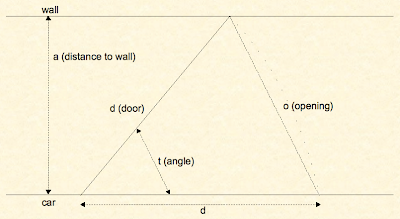
Suppose I park my car in a garage. The side of the car is some fixed distance from the garage wall, limiting the amount that the door can open. Figure 1 illustrates that: the car is parked at a distance of a from the wall (because mathematicians like to confuse things by representing everything with incomprehensible letters), the door has a length of d, and when the edge of the door hits the wall, the angle the door makes with the car is t. (Click on the figures to enlarge them.)
Figure 1
What we want to know is how big the opening (o, in figure 1) is, so we know how easy it will be for a person to get in when the door is as far open as it can be. Noting that the closed-door position, the open door, and the opening form a triangle, we bet we can sort this out with trigonometry.
The first step is to drop a line from the tip of the door to the car, perpendicular to the car. The dashed line labelled a in figure 2 forms a right triangle.
With respect to angle t, the opposite side has length a and the hypotenuse has length d. The sine of the angle, sin(t), is the opposite side divided by the hypotenuse, or a/d. So we have our first formula, which we can solve for t:Figure 2
sin(t) = a / dt = arcsin(a / d)
Now we’ll note that the two sides of length d form an isosceles triangle with base o. That means that if we bisect angle t we’ll get two equivalent right triangles (figure 3).
We now have an angle t/2, a hypotenuse d, and an opposite side o/2, giving us our second formula, which we can solve for o:Figure 3
sin(t / 2) = (o / 2) / do = 2 * d * sin(t / 2)
It’s time to plug in the numbers.
Let’s assume that a four-door car’s front door is 4 feet long, and a two-door car’s door is 6 feet long. And let’s say we park the car 3 feet from the wall. So, for a 4-door car:
a = 36 in, d = 48 inAnd for a 2-door car:sin(t) = 36 in / 48 in
t = arcsin(36 / 48) = arcsin(.75) = 48.59 degrees
sin(48.59 / 2) = (o / 2) / 48 in
o = 2 * 48 in * sin(24.295) = 2 * 48 in * .41143 = 39.5 in
a = 36 in, d = 72 insin(t) = 36 in / 72 in
t = arcsin(36 / 72) = arcsin(.5) = 30.00 degrees
sin(30 / 2) = (o / 2) / 72 in
o = 2 * 72 in * sin(15) = 2 * 72 in * .25882 = 37.27 in
So, though the door on the two-door car is longer, with the wall restricting it the door will create an opening that’s about two and a quarter inches (5.6%) smaller. That’s actually less of a difference than I’d expected. It was good to do the exercise, which showed that I was right... but not by enough to matter.
[1] I love that blog name!
[2] Demonstrating, as it does, why we mathematicians are in such demand at parties.








8 comments:
I imagine that it's more significant if you have someone in the back seat, though...
Oh, two-door cars are miserable for back-seat access, and my friend fully acknowledges that. But as I said in the post, he doesn't have people in the back seat often, and he'd rather make the access to the front easier.
Yes, you guys are RIGHT up there with engineers at parties. I have a biologist friend who is married to an accountant, and for some reason he tells her that her friends and co-workers are MUCH more fun than his.
If I'm reading the problem right, you could use Law of Cosines from the very beginning right? That would be a nice quick problem for students studying that.
I beg to differ. What you have solved for, I believe you will realize when you look at your diagrams, is NOT the minimum opening. If you re-think the problem and re-examine the triangles you will get a rather surprising result. With that result in hand you will then be looking for another factor that might account for the "believed by everybody fact" that long-doored cars are harder to exit. Consideration of the thickness of the door does not get you anywhere, either. There is yet another factor, and you will probably do a H. Simpson "Doh" when you realize it...I will not spill the beans just yet!
Doesn't two-door cars have bigger-by-length doors?
it's very interesting. I think two-door cars are perfect.
He-he. Zoomer Daily is a web site about car racing. Yes, I see how they wouldn't worry too much about this aspect of things....
Post a Comment